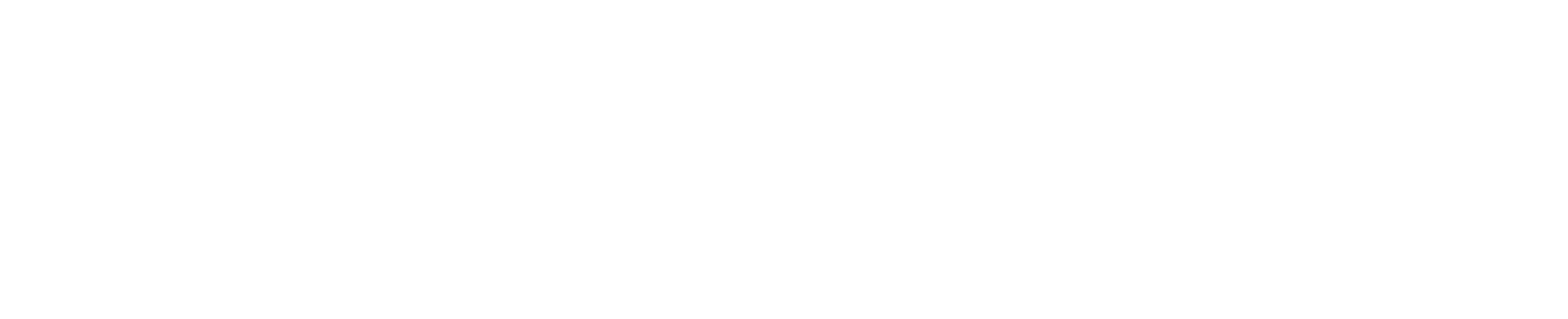a \times b=b \times a
当ブログは、自閉スペクトラム症の当事者である僕が、いつも見ている世界をできるだけ詳細に言葉にすることで、皆さんに他者の価値観を鑑賞していただく試みです。
この記事は、Amebaブログのリメイクです。
ネットでよく話題になっている、かけ算の順序問題。
車が5台あります。
1台につき4人乗ることができます。
このとき、全部で何人乗れますか?
このような、小学2年生の文章題で、
5 \times 4 = 20という途中式を書いた解答に「不正解」だとバツをつける教員の是非について、議論がなされているのを見たことがあるかな?
不正解にする根拠としては、かけられる数(前半)を「一つあたりの数」・かける数(後半)を「いくつあるか」とするルールに基づいて、4\times 5 のみが正答であるというもの。
これが「理不尽だ!」「無駄な教育だ!」って顰蹙を買っているのをよく見るんだ。
…正直、どうでもいいって?
そう言いたい気持ちもわかるんだけど、今回は、真面目に数学的な観点と教育的な観点から考察して、僕なりの意見を話していこうと思うよ。
交換法則って自明なの?
かけ算ってひっくり返しても答えは同じだし、気にする必要あるの?
任意の二数で、かけ算の順序をひっくり返しても、積の値は変わらないというのは、かけ算を習いたての小学生にとっても当たり前かな?
任意の二元 x,\, y が演算 R について
x\,R\,y=y\,R\,x
となるとき、演算 R は交換法則を満たす(可換である)という。
かけ算(×)についても、この交換法則が満たされることを確認するのは、なかなか大変だよ。
普通、最初にかけ算を習うとき、「かけ算はたし算をたくさん書くことを省略するための計算だ」と説明するよね。
3 \times 5 = 3+3+3+3+3
a \times n = a+a+ \cdots +a( n 個)
という「かけられる数」が「かける数」の分だけ足し合わされているというのは、習いたての小学生にも分かりやすい“定義”だよね。
これを考えると「かけられる数」と「かける数」には、かなりの違いがある。
もう少し学年が進んだあとで、小数を習ったとして、
3.6 \times 4 は、3.6 を 4 つ足せばいいから、3.6+3.6+3.6+3.6 として考えられそうだけど、 4 \times 3.6 は、どうだろう?
4 が 3.6 個分…ってどういう意味だ?
ね、交換できるのって全然当たり前じゃない気がするでしょ。
でも一応、自然数同士のかけ算なら、数学的帰納法によって簡単に説明できるから、気になる人は下記をクリックして見てみてね。
前提として、
加法の結合法則:(a+b)+c=a+(b+c)
加法の交換法則:a+b=b+a
を認める。これによって、加法については並び替えが自由にできる。
任意の自然数 a, \,b, \,c について、
\begin{split} (a+b)\times c &= (a+b)+(a+b)+ \cdots +(a+b) \\ &= a+b+a+b+ \cdots +a+b \\ &= (a+a+ \cdots +a)+(b+b+ \cdots +b)\\ &= a \times c+b \times c \end{split}「(a+b) が c 個」を「a が c 個、b が c 個」に書き換えているだけ。
また、同様に、
\begin{split} c\times (a+b) &= c+c+ \cdots +c \\ &= (c+c+ \cdots +c)+(c+c+ \cdots +c) \\ &= c \times a+c \times b \end{split}「 (a+b) 個」とは、「a 個 と b 個」と考えられる。
つまり、次のように分配法則が示せる。
\begin{split} (a+b)\times c &= a \times c+b \times c \\ c\times (a+b) &= c \times a+c \times b \end{split}(ここまでが準備)
任意の自然数 m, \,n について、m\times n = n\times m であることを証明する。
ここで、m\times 1 = m(∵ m が 1 個だけあるということは、m自身)
同様に、1\times m = m(∵ 1 が m 個あるということは、m自身)
よって、n = 1 では成り立つ。
次に、n = k のときに成り立つと仮定する。(m\times k = k\times m)
m\times (k+1) について、分配法則と仮定により、次の式変形ができる。
したがって、m\times (k+1)=(k+1)\times m と言える。
数学的帰納法より、m\times n=n \times m が示された。
そこまで厳密ではないけど、それなりに納得できるんじゃないかな。
じゃあ「かけられる数」「かける数」がどっちがどっちだったか忘れちゃったときは、この証明をテストの余白に書いておいたらいいんだね。
小学生が書く想像はつかないけど、これなら確かに文句を言う先生はいないね。
ただ、さっきの 4 \times 3.6 みたいに、たとえば「リボンの長さ」や「液体の量」のような実数全体で考えたいときは、やはり交換法則を考えるのは難しいよね。
まあ、群・環・体とかをちゃんと学んでもらうと、もう少し実感できると思うんだけど、実数に関する乗法の可換性は前提(公理)としてしまうことが多いから、証明したりするようなものではなかったりもする。
要するに、かけ算の交換法則は自明ではない!
もちろん、長方形の面積を「たて×よこ」としたときに、見る方向を変えても面積は変わらないなんて説明をすることもできるけど、それなら“面積”の定義はなんですか?って感じになるから、ちょっとやめておこう。
そう思うと、この「かけ算の順序問題」は、先生側にも一理あるってわかるよね。
答えが合っていれば、式はなんでもいい!なんてことはない。
もしも、さっきの 4\times 5 の問題を 3+6+11 とか 32-12 みたいな謎の途中式を書いていたら、たとえ答えが 20 であっても、正解にはしづらいと感じられるんじゃないかな。
反対に書く意味はある?
でもさ、かけ算の順序を間違えるのと、3+6+11 みたいな意味わかんない式を書くのとでは、さすがに大きく違う気がするんだけど、どうなんだろう?
車が5台あります。
1台につき4人乗ることができます。
このとき、全部で何人乗れますか?
って問題だったね。確かに 3+6+11 は意味不明だけど、5\times 4 の方はそれが正しい式だと解釈することも、実はできるんだ。ちょっとその一例を考えてみるよ。
5×4の解釈例えば、車の4つの座席に、それぞれ A席、B席、C席、D席と名前をつけておく。
すると、5台の車がある分、A席は5席、B席も5席、C席も5席、D席も5席あるから、1種類あたり5席あって、それが4種あり 5×4 となる。
こんな説明ならどうかな?
こういう解釈を初めからするとは考えにくいけど、意外とできるもんだよね。もちろん連続的な量を取る「リボンの長さ」などには使えないし、対象によってしまうのは仕方ないけどね。
あとさ、これは感覚的な話なんだけど、中学生以降で文字式か出てくると、少し順序の意味合いが変わってくるような気がする。k 円のケーキを 3つ買ったときは、3k 円って書きそうだよね。3倍の k 円みたいな意味なのかな。
それに、日本とは逆にすることが自然な言語圏もあって「4\times 100mリレー」はもちろん、4mを100人で走るわけではない。
だから、そもそも「かけられる数」を前に書くみたいなルールも別にあってないようなものなのかもしれないね。
だとしたら、先生のバツが嫌になっちゃうよ!
そうだよね。じゃあ、先生はかけ算の順序問題に対して、どんな指導をしたらいいんだろう?
何が大切かわかるかな?
僕の専門は、中等数学教育(中高生の数学)であって、小学校の算数の教育についてはあまり知らないから、頓珍漢なことを言っていたら申し訳ないんだけど…。
確かな学力の育成のためには、自ら考え、自ら学ぶ力が大切だとされているよね。それに、対話的な学びが重要視されるなか、「正解」「不正解」だけで学習の機会を片付けること自体が、あまりよくないと思ってしまうな。
児童生徒がせっかくしたミスは、できるだけ学習の機会にしたいものだし、しっかりと「なんでこの順番で書いたの?」と尋ねてみるのがいいと思うよ。
そうしたら「かけ算が自明に交換法則を満たす」とは言えないことを、自ら感じられるかもしれないし、かけ算の本質的な意味について考えようとするきっかけになるかもしれない。
すべての指導は、その学習の目標に対する目的をもって行われるべきで、「ルールと違うから」という理由だけで、問答無用で単に不正解にするというのはどういう目的があるか不明だよね。
じゃあ、そういう先生は、物事の理由なんて何も考えず、とにかくルールに従うような社会の奴隷にできる人間を育成したいっていう目的で指導しているのかな?
(言いにくい過激なことをモラリに言わせているかも…?)
かけ算の文章題を用いて、達成したい目標は
- 乗法の意味について理解し、それが用いられる場合について知ること。
- 乗法が用いられる場面を式に表したり、式を読み取ったりすること。
- 乗法に関して成り立つ簡単な性質について理解すること。
- 性質を活用して、計算を工夫したり計算の確かめをしたりすること。
- 数量の関係に着目し、計算の意味や計算の仕方を考えること。
- 数量の関係に着目し、計算を日常生活に生かすこと。
とされている。
ちなみに【算数編】小学校学習指導要領(平成29年告示)解説では、「成り立つ簡単な性質」に「交換法則」を挙げ、計算を確かめる場合には「交換法則」を用いてもよいってしているよ。
でも、その一方で
被乗数と乗数の順序は,「一つ分の大きさの幾つ分かに当たる大きさを求める」という日常生活などの問題の場面を式で表現する場合に大切にすべきことである。
引用:【算数編】小学校学習指導要領(平成29年告示)解説 P115
とも(かなり分かりにくい文章だが…)述べられているから、交換法則は計算の工夫でしかないって意味に感じるね。
かけ算では、5の段の方が先に習うから、4の段より5の段の方が簡単だと言える。そこで、さっきの問題は、4\times 5 =5\times 4 =20 と「工夫した」と言うのも許されるかもしれないね。
「かけ算の順序」を大切にした方がいいのは、式で表現するときに、意味を考えやすくなるようにするための指導の工夫であって、引っ掛け問題で子どもたちの注意力を上げるとか、そういうためのものではないんだよね。
不正解にされると、モチベーションが下がるってこともあるから、日常生活に対して主体的に学んだことを活かしたいと思えるような関心を養うには、数学的な見方・考え方(小学校では言わないかも)を働かせられるように、点数は与えながら、どのように考えて立式したかと説明させたり、そういった解答をテスト後に取り上げて、「なぜかけ算は順番が大切か」「こういうミスが起きやすかったのはなぜか」のような議題をグループワークで話し合わせるなど、次の学習に繋げることが大切だと、僕は思ったよ。
うーん、なんか、無駄に熱くなってしまった…。みんなも算数・数学の指導について考えたことや、悩むことがあったら、ぜひ教えてね。それじゃあ、またね。