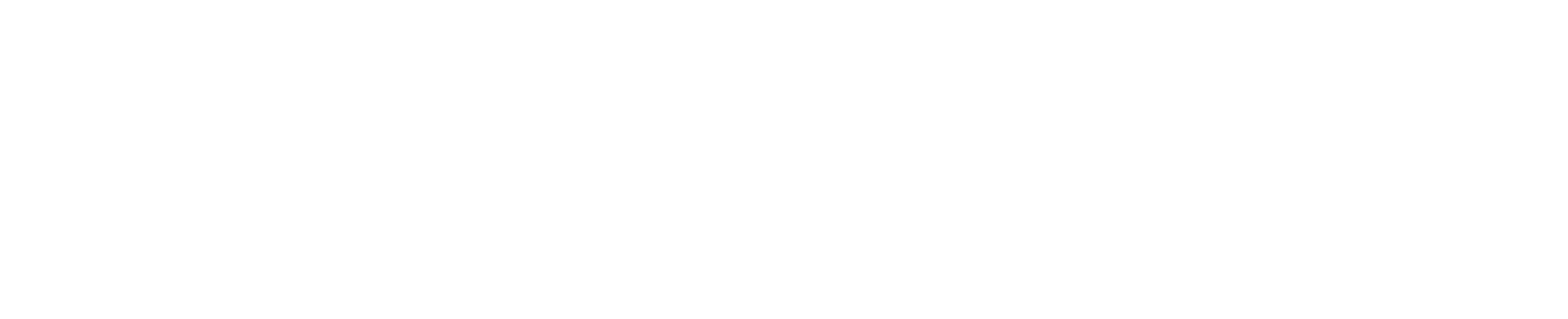18 \div 0=
当ブログは、自閉スペクトラム症の当事者である僕が、いつも見ている世界をできるだけ詳細に言葉にすることで、皆さんに他者の価値観を鑑賞していただく試みです。
この記事は、Amebaブログのリメイクです。
ネットでよく話題になっている、ゼロ除算。
18÷0=
という、算数の問題に対して「こたえなし」と書いたら、不正解にされたと言う内容のツイートが流行っていたよね。
この答えは0じゃないの?
a÷b の割り算というのは「a の容量入れ物に b はいくつ入るか」というイメージで考えるといいよ。
それじゃあ、18のなかに0はいくつ入るかってことなんだね。
うーん、それならいくらでも入るじゃん。無限大とか…?
無限大は数ではないし、このような「ゼロで割る」という行為は普通の数の体系では「定義されない」とするのが一般的なんだ。というか、この事実は僕の感覚的には、除法ないし、四則演算全体において、最も重要なことだと感じているよ。
(群・環・体とか代数の勉強をするとちょっとしてみると共感してもらえるかも)
じゃあ「こたえなし」って解答は結構いいんじゃない?
そうだね。等式は「左右の値が等しい」ということを単に「示す」だけのものだから、「こたえ」というのが何のことか、本当は議論する必要があるけどね。
数学的に言うなら「この等式の左辺は定義されない」のような書き方で、欄外とかに書くのが無難だと思うよ。
今日は数学的な話はあまりする気がないけれど、数学的に何がいけないのか一応少し感覚的な解説をしておくね。
掛け算を定義した後に、
「b×c=a であるとき、a÷b=c とする。」
というのを割り算の定義としてみよう。
そこで、18÷0 = k と置いてみると、
k は、0×k = 18 となるような k であることがわかるけれど、任意の実数は0を掛けると0になるということは、掛け算までの定義で証明できるから、存在しないと言えるんだ。
このように、解が存在しない方程式を不能な方程式というよ。
また、0÷0 = k と置いてみると、
kは、0×k = 0 となるような k であることがわかって、これは k がいかなる実数であっても満たすと言えるね。
このように、解が複数存在する方程式を不定な方程式というよ。
これは、数の概念の中でかなり重大な欠陥になってしまうんだ。
できない計算があるというのも大きな問題だけど、特に0÷0がどんな数にでもなり得るとなると「1=0÷0=2 より 1=2」みたいな、どんな数でも等号で結べるという「数の概念の破壊」が起きてしまうんだ。
(本当は掛け算を定義するときに「逆数」が必要になって、0の逆数が存在しないという議論をする必要があるけどね)
ただ、文字が入ってないと“方程式”ではない。だから、18÷0に対してTwitterなどでは、「解なし」という解答もよく見るけれど、「解」が方程式に対応するものだと考えると、相応しくないから気をつけてね。
この記事で書いたこともあったように、小学校の先生はそれぞれ専門教科があって、それが数学ではない先生ももちろんいるから、この「数学にとっての重要性」が算数では無視されてしまう場合があるんだと思う。
特に数学は、人によって解釈が分かれることがあまりない論理的な性格を持つから、その教科における教育については知らないという人からも、簡単に指摘されることが多いんだろうね。
僕も、国語や社会や体育やら…なんでも全部教えろと言われたら、どれか一つくらいは“おかしな”教え方をしてしまう気がするけれど「完全に間違っている」とは言い難いものがほとんどだろうから、問題にはならないというケースもあると思うのよね。
それにしても、算数を「数学をしっかり学ぶための準備としての教育」と見ると「ゼロで割らない」ということの意義を理解させること(もしくは理解までいかなくても「なんとなく絶対割ってはならないんだ」と気をつけさせること)は、重要だと言えるけれど「日常生活に割り算を活かすための教育」と見ると、別にそんなことはどうだっていいのかもしれないね。スーパーに行って「12個入りのお菓子を0人で分けたいな」とか、思うときなんてないし…。
算数で目標とする力は、この日常的に数的処理ができることの方であるから、こういう「数学者」との齟齬が生まれるのかもしれない。
「算数」と「数学」は地続きな学習ではあるけど、目標は違うんだね。
恨むなら学習指導要領からだね。
学問と真摯に向き合っている人ほど、小学校で適当に“間違って”教えられることを嫌がるかもしれないけれど、障害児教育なんかを考えれば、この「生活に学問の内容を使える」という単なるスキルを涵養することも、もっと大切に感じてくると思うよ。
ただ、僕はこの18÷0のツイート見たとき「さすがに釣りか?」って思ってしまったんだよね。この「ゼロ除算」なんていうのは、もうさすがに誰もそんなことしないだろと思えるくらいに、僕の中では「当たり前の禁忌」だったからさ。さすがに数学が専門でないにしても、これを知らない教師などいなかろうと思ってしまったんだ。
ただ、この動画を見て、ゼロ除算ってそこまで“常識”ではないのかもしれないと気がついたんだ。
なんか「認識」とか「小学生のうちは」みたいな意見を言っているんだけど、高学歴が売りの二人でも、このゼロ除算の禁忌については、“常識”のように扱う内容ではないのかと、少しばかり驚きだったんだ。
倫理観や価値観とか、そういうものには人それぞれの見方があって、“常識”などなかろうと思っているんだけど、単なる知識のレベルでも自分が“常識”だと思っていても、そうでないものはたくさんあるんだなと思わされた。
その界隈では常識になっていて、ここが「世界」なのか「何かしらの界隈」なのかってわかりづらい場合もある気がするね。
教育というのは「自分が知っていること」を「まだ知らない人」に伝えるというのが根幹にある活動だけど、これを踏まえると、すべての分野においては、可能でない気がして悩ましくなる。
自分が知っていることが“常識”ではないということを、僕たちはどうやって認識すればいいんだろうね。「数学を教える」というのは、内容が決まっていて、まだ楽なもんだけど…。