「平方数」〜数学好きが2025年を迎える準備

2025の性質

　当ブログは、自閉スペクトラム症の当事者である僕が、いつも見ている世界をできるだけ詳細に言葉にすることで、皆さんに他者の価値観を鑑賞していただく試みです。

---

　もうすぐ2025年、もう年末年始の予定は立てているかな？

　数学の入試問題では、整数としてその年の値を使った問題が出ることも多いもんだから、数学好きのみんなは、次の年の数字にまつわる性質や問題を集めないと年を越せないって人も多いよね。

いやいや！そんな人、聞いたことないよ。
まぁ、​素因数分解くらいならするかもしれないけど…。

　でも大抵の数学好きは、生きている間にあり得る西暦の年号くらいなら、小さいときにすべて素因数分解を終えてしまっているだろうし、それくらいじゃ満足できないよね。今回は数「2025」の性質を深掘りしていくよ。

2025は平方数

　それに、まとめて数百個の素因数分解をしたことはないという人も、毎年素因数分解をしていれば、2025が平方数（ある自然数の2乗として表せる数）であることは、既知だと思う。

　1989年や2009年、特に最近の、2021年、2024年には、平方の差が和と差の積に因数分解できることを用いて、

　みたいな素因数分解のために、2025 = 45² を使ってきたもんね。

それをしてきた人からすると、待ちに待った2025年だね。

　ちなみに、本日12月25日はハロウィン…じゃなくて、クリスマス（※僕はクリスマスハロウィンといいます）だけど、この1225も35²という平方数だね。

　4桁で日付を表すとき、平方数になるのは、

　の、8日間。来年のこれらの日付はみんなでパーティでもしようね。でも、4月9日は、4も9も49も平方数だから、こちらの方が平方数パーティには適しているかな。

意外とたくさんあるんだね。
平方数って、そんなに多くあるなら、西暦が平方数になるのもそんなに珍しくないんじゃないの？

　いやいや、平方数は数が大きくなると、少しずつスカスカになっていく。

　n² と (n+1)² の差は、(n²+2n+1)-(n²) = 2n+1 だから、45²から46²までは、45×2+1で、91も離れていることが分かる。つまりは、あと91年も平方数の年号はやって来ないってことだ。前回は89年前だし、一生に一度って人も多そうだよね。

総和の考え方を使う

平方数の差が 2n+1 になるってことは、これは奇数の一般項と言えるから、1から、ある奇数までの総和は、必ず平方数になっているんだね。

　そうだね。n 番目の平方数は、1 からn 番目の奇数までの総和って言えるから、2025も45番目の奇数までの総和として表せるよ。（2025 = 1+3+5+ … +87+89）

　また、特に45の方に注目してみると、これは、9番目の三角数（1からある自然数までの総和として表せる数）だよね。（1+2+3+4+5+6+7+8+9=45）
　ここで、数学Ｂを学んだことがある人は、総和の公式を思い出してみよう。

　注目して欲しいのは、一番下の「3乗の総和の公式」
　2乗されている中身が、自然数の総和の公式とまったく同じだから、

　だと言えるよね。つまり、n 番目の三角数の平方は、n 番目までの立方数の総和だと言えて、45という三角数の平方である2025は、

 2025 = 1³+2³+3³+4³+5³+6³+7³+8³+9³

　と、立方数の総和としても表せるんだね。

九九と2025

少し見方を変えて、45×45を単純に

　と見て、一つずつ展開することを考えれば

　と変形できると分かるよね。

これって、九九で出てくる積の数字の総和になるってことだね！

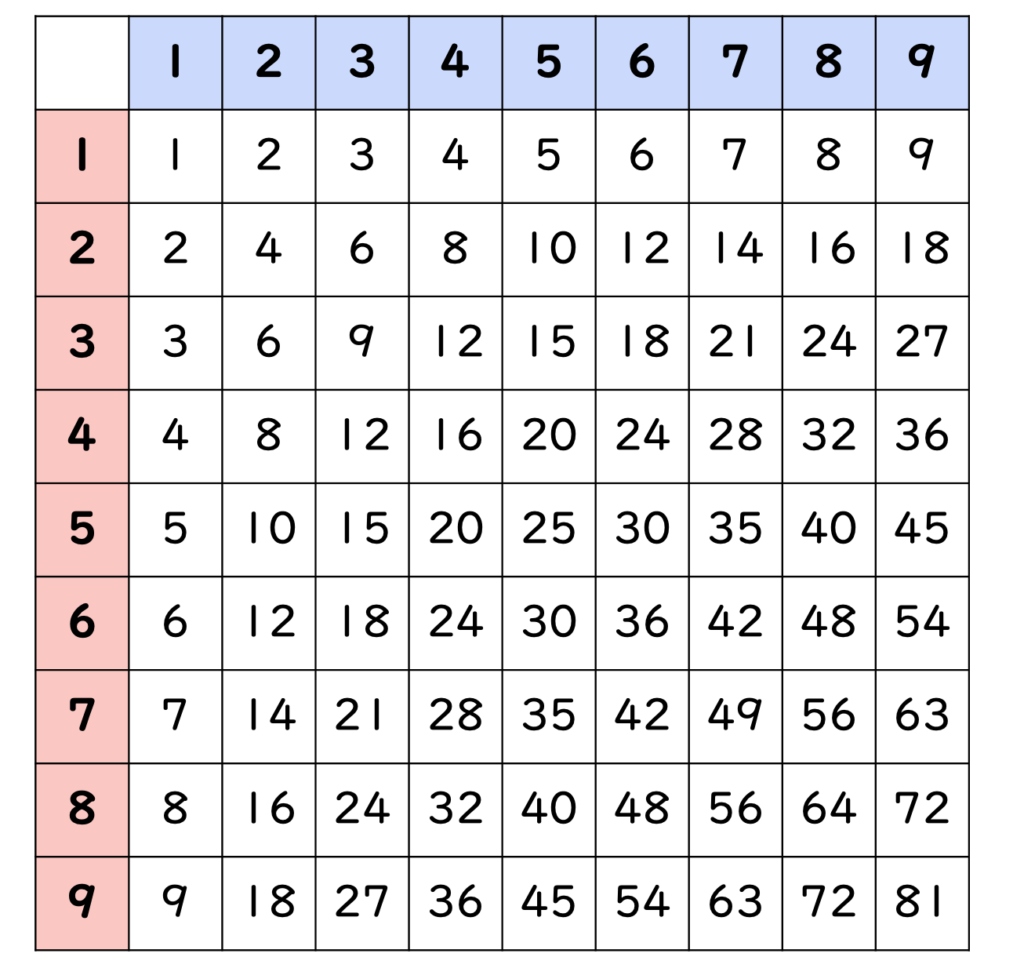
　これが一番面白い性質だと感じるなぁ。ほぼ真ん中に 20 25 があるのも運命かも…。
　九九の表の総和が2025になることを問題として求めさせるのも面白いし、その小問として九九の表にまつわる問題も、たくさん作れそうだよね。2025年に試験を受ける人は対策してみてね。

その他いろいろな性質

　このように、2025が45²であることを用いて考えるだけでも、なかなか奥深いんだけど、他にも2025には面白い性質があるから、紹介だけしようと思う。もうちょっと変化球な問題を作りたいって人は、利用してみてね。

(20+25)² = 2025 カプレカ数

　カプレカ数には全然違う二つの定義があるんだけど、そのうちの一つが

　というものなんだ。例えば、45²の2025を、2+025や20+25、202+5のように分けて、45そのものに戻すことができれば、カプレカ数であるということだね。確かに、20+25=45だから、45はカプレカ数になっている。

　このような数は、他には55や297、703なんかが知られているけれど、問題にするなら、「9999のような9を繰り返した数は、必ずカプレカ数になることを証明しよう」とかかな。2025にまつわる問題としては、かなりトリッキーだけど、僕に受験問題を作らせてくれるなら、必ず入れたいと思う一問だよ。

各位に1を加えた 3136 = 56²

　各位に1を加えた数も平方数になるという性質を持つ平方数は、1番目が25、2番目が2025だから、それなりにレアな性質だよね。問題として出すなら、

「このような性質を持つ数の下二桁は25に限られるということを証明しよう」

　なんてどうだろう。これだけだとちょっと難しいから「平方数の下二桁が共に奇数になることはないことを証明しよう」とかを誘導の問題としてつけてもいいかもしれない。もしよかったら、やってみてね。

81/400=0.2025

　小数として表すとこうなるんだけど、よーくみると

3⁴/(3⁰+3¹+3²+3³)=2.025

　と、3だけを使って、結構きれいに表せることがわかるね。
　4000と言えば、7⁰+7¹+7²+7³ と表すこともできるね。3か7を使えるような確率の問題で、こんな状況を作り出せたら面白いかもしれない。それに、確率なら分数で答えるのが普通だから、2025は密かに忍ばせることができるね。恥ずかしがり屋の出題者さんはぜひ作ってみよう。

2025と3751

　最後は、問題にはしづらいけど、面白い性質を見つけたから紹介するね。

　っていう、ちょっとした奇跡。ノートでひたすら2025と格闘しているときに見つけて驚いたけれど、これと言って使い道がない不遇な性質だな。

クリハロくんが、気持ち悪いぐらいにいつも数字のことばかり考えているんだってことはよく分かったよ。

　数学の問題にならないかな〜って思いながら、日常生活を送っていると、数学の問題を解くことくらいなら、すこぶる簡単になってくるもんだよ。作り手目線で問題に向き合うと、そんな発見があると思うから、みんなも数字や、数学的な現象とお友だちになってみてね。

　さて、みんなもこれくらいで2025年を迎える準備ができたって言えるかな。その他にも2025にまつわる面白い性質があったら、ぜひ教えてほしいな。来年がちょっと楽しみになったね。

---

---